Методические рекомендации по проведению лекционных занятий с применением информационных технологий

Теорема: Если векторное поле представляет собой преобразование областей , то кусочно-гладкая поверхность, лежащая в области преобразуется в кусочно-гладкую поверхность, лежащую в области .

Как и в случае двух переменных эта теорема позволяет трактовать преобразование как переход от ПДСК к КСК.

Криволинейные координаты в трехмерном пространстве будут уже являться криволинейными координатными поверхностями.

И сетка будет задаваться криволинейными поверхностями.

Координатные поверхности в КСК могут быть заданы параметрически следующим образом:

а) зафиксируем , тогда пространство будет задаваться

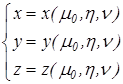
где , а является параметром при создании этой кривой поверхности.

б)

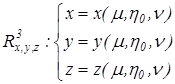
где , а является параметром.

в)

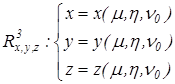
где , а является параметром.

5.Уравнение связи из ПДСК в КСК имеет вид:

.

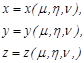
Аналогично записывается уравнение связи из КСК в ПДСК .

Цилиндрическая система координат

1. Векторное поле в данном случае задается

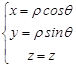
где , , .

2. Пусть дана точка .

3. Спроектируем ее на плоскость , т.е. найдем .

4. называется полярным радиусом, - полярный угол.

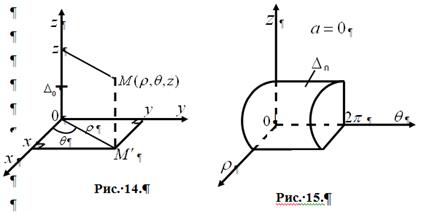
5.Для получения взаимно однозначного соответствия между ЦСК и ПДСК нужно вырезать ось : .

Методы и формы организации профессионального воспитания учащихся
Профессиональное воспитание включает в себя формирование склонностей и профессиональных интересов учащихся. Сущность педагогической работы по профессиональному воспитанию заключается в том, чтобы побуждать учащихся к участию в разнообразных формах учебной и внеклассной работы, общественно-полезному ...

Практическое применение форм внеурочного воспитания
Внеурочная воспитательная работа в классных коллективах проводится в традиционных для школы формах по следующим направлениям: 1) учебно-познавательное: -предметная неделя русского языка; -библиотечные часы; -конкурсы, олимпиады, игры и другие учебно-познавательные мероприятия. 2) культурно-просвети ...

Философско-мировоззренческая подготовка школьников
Научные знания выступают как часть, сторона, подтверждение диалектического взгляда на мир. Рассматривая научное мировоззрение как способ осмысления, понимания и оценки объективной реальности, мы обнаруживаем, что оно представляет собой связь между различными знаниями, идеями, понятиями, образующими ...