Методические рекомендации по проведению лекционных занятий с применением информационных технологий

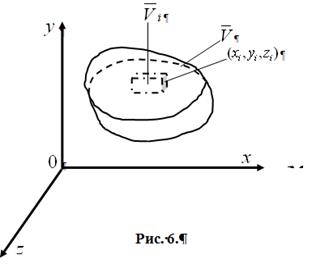
5.Обозначим через диаметр , максимальное расстояние между точками, а - наибольший из всех диаметров частичной области , , -ранг разбиения области на частичные области .

6.Выберем в каждой частичной области произвольную точку .

7.Составим интегральную сумму вида:

,

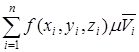где - мера объема (мера Жордано).

Определение: Если при , интегральная сумма стремиться к конечному пределу, причем он не зависит от способа разбиения тела на подобласти и выбора точек , то функция называется интегрируемой по области , а сам предел называется тройным интегралом от функции по области и обозначается

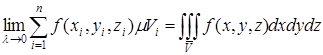[2].

Свойства тройного интеграла

1. Если функция интегрируема по области , то она ограничена на указанной области.

2. Если функция непрерывна по области , то она интегрируема на указанной области.

3. Если область разбита на две, то тройной интеграл равен сумме тройных интегралов, т.е. если , то

.

Существование интегралов в правой части обеспечивает существование интеграла в левой части и наоборот.

4. Если - некоторое действительное число (), то константу можно выносить из под знака интеграла . Если f - интегрируема, то и функция интегрируема, если . Из существования интеграла в левой части вытекает существование интеграла в правой части.

Особенности процесса самообразования воспитателя дошкольного образовательного учреждения
В настоящее время становится все более очевидным, что осуществление процессов модернизации образования с необходимостью требует актуализации личностного и профессионального потенциала педагогов. Именно концентрация сил на создании условий для понимания и принятия педагогами целей и содержания обнов ...

Специфика организаторской деятельности педагога
Специфика организаторской деятельности педагога проявляется прежде всего в ее целях. Она не имеет конкретного предметного результата, который можно было бы воспринимать с помощью органов чувств, поскольку направлена на обеспечение эффективности других видов деятельности (учебной, трудовой, научной) ...

Результаты проведения исследования
Итоговые результаты первого исследования представлены в таблице 1 в виде процентного выражения количеств правильных ответов (по двум годам). Таблица 1 Годы Группы 1 2 2008/2009 20,2 19,6 2009/2010 17,7 16,6 Как видно из приведенной таблицы, за два года, прошедших с начала эксперимента, уровень разв ...