Методические рекомендации по проведению лекционных занятий с применением информационных технологий

2.Тогда область разобьется кусочно-гладкими границами на частичные области , .

3.Составим интегральную сумму такого рода

,

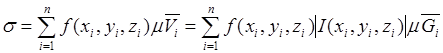так как

и на основании 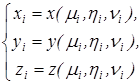справедливы формулы

.

Интегральную сумму можно переписать в таком виде

4..

5.Если перейти к пределу при от левой части формулы п.3 и от правой части п.4, то получится требуемое выражение, ч.т.д .

Объем в ЦСК и ССК

1.В ЦСК объем вычисляется по формуле:

.

2. В ССК объем вычисляется по формуле:

.

3.4 Методические рекомендации по проведению практических занятий

тройной интеграл педагогический студент

При изучении курса «Математический анализ» студенты часть материала должны проработать самостоятельно. Роль самостоятельной работы велика.

Планирование самостоятельной работы студентов по курсу «Математический анализ» необходимо проводить в соответствии с уровнем подготовки студентов к изучаемому курсу. Самостоятельная работа студентов распадается на два самостоятельных направления: на изучение и освоение теоретического лекционного материала, и на освоение методики решения задач по математическому анализу.

В помощь студенту здесь могут быть рекомендованы фондовые лекции, которые разрабатывает ведущий преподаватель курса. Фондовые лекции представлены в распечатанном и набраны в электронном видах. При всех формах самостоятельной работы студент может получить разъяснения по непонятным вопросам у преподавателя на индивидуальных консультациях в соответствии с графиком консультаций. Студент может также обратиться к рекомендуемым преподавателем учебникам, учебным пособиям и обучающе – контролирующей программе, в которых теоретические вопросы изложены более широко и подробно, чем на лекциях и с достаточным обоснованием.

Консультация – активная форма учебной деятельности в педагогическом вузе. Консультацию предваряет самостоятельное изучение студентом литературы по определенной теме. Качество консультации зависит от степени подготовки студентов и остроты поставленных перед преподавателем вопросов.

Основной частью самостоятельной работы студента является его систематическая подготовка к практическим занятиям. Студенты должны быть нацелены на важность качественной подготовки к таким занятиям. При подготовке к практическим занятиям студенты могут пользоваться разработанными «Методическими рекомендациями к практическим занятиям» по курсу «Математический анализ» и задачниками. Кроме того, можно воспользоваться электронным пособием по теме “Тройные интегралы” . Планы практических занятий и заданий к ним приведены в «Методических рекомендациях к практическим занятиям».

Особенности формирования культуры межнационального общения у младших подростков
Культура межнациональных отношений - есть не что иное, как высокая степень совершенства и развития этих отношений, которые проявляются в межнациональных экономических и духовных связях разных народов, в соблюдении определенного нравственного такта и взаимной уважительности представителей различных ...

Развитие процессов мышления и понимания в рамках культурно исторической концепции
Концепция разрабатывалась Выготским и его школой (Леонтьев, Лурия и др.) в 20-30 гг. XX в. Одной из первых публикаций была статья "Проблема культурного развития ребенка" в журнале "Педология" в 1928 г. Следуя идее общественно-исторической природы психики, Выготский совершает пер ...

Факультативные занятия как один из компонентов дифференцированного обучения
факультативное занятие математика нестандартное решение Дифференциация обучения – это необходимое условие гуманизации и демократизации образования. Она предоставляет каждому учащемуся равно высокий шанс достичь высот культуры и является залогом максимального развития детей с самыми разными способно ...