Методические рекомендации по проведению лекционных занятий с применением информационных технологий

6. Уравнение связи ЦСК с ПДСК имеет вид: . Такая система координат называется цилиндрической, т.к. одна из ее координатных поверхностей является цилиндром.

7. Координатные поверхности в ЦСК:

- цилиндры, - полуплоскости, - плоскости.

8. Функциональный определитель в ЦСК имеет вид:

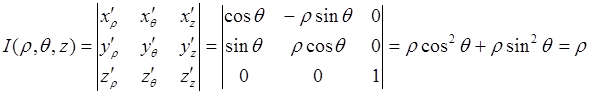, [3].

Сферическая система координат

1.Векторное поле в данном случае задается

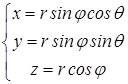
где , , .

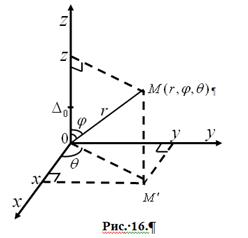
2.ССК организована в пространстве .

3.Уравнение связи ССК с ПДСК имеет вид: .

4.Координатные поверхности в ЦСК:

- сфера, - круговой конус, - полуплоскость.

5.Функциональный определитель в ССК имеет вид:

,

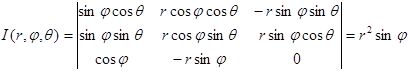[3].

Замена переменных в тройном интеграле

1.Пусть непрерывна в замкнутой области с кусочно-гладкой границей.

2.Пусть векторное поле осуществляет преобразование пространства

, в котором содержится в , а содержится в и - кусочно-гладкая граница одного поля, - другого.

3.Пусть области и - ограниченные области, т.е. они будут измеримы по Жордано – кубируемы (имеют объемы).

4.При всех указанных условиях будет справедлива формула:

.

Доказательство:

1.Разобьем область на подобласти кусочно-гладкими поверхностями .

Характеристика практических методов обучения
В процессе обучения большое значение имеет выра­ботка у учащихся умений и навыков применения полученных знаний на практике. Метод упражнений. Умения и навыки формируются с помощью метода упражнений. Сущность этого метода состоит в том, что учащиеся производят многократные действия, т.е. тренируются ...

Этапы научно-исследовательской работы студентов
Научно-исследовательскую работу можно условно разделить на три этапа: констатирующий, обучающий, контрольный. Начальный этап констатирующий, включает выбор темы исследования; постановку цели и задач исследования; изучение реальной практики по решению поставленной проблемы; изучение существующих в т ...

Методика проведения экспериментальных уроков курса «Основы безопасности жизнедеятельности» в 8-м классе
Рассмотрим, как происходило включение системы заданий краеведческого характера при изучении курса «Основы безопасности жизнедеятельности» (Раздел 1. «Безопасность и защита человека в чрезвычайных ситуациях») 8 класса в экспериментальном обучении. Поурочное планирование [15, 19, 20, 32] курса «Основ ...