Методические рекомендации по проведению лекционных занятий с применением информационных технологий

5. Справедлива формула:

.

Существование интегралов в правой части влечет существование интеграла в левой части.

6. Если и они интегрируемы на , то

.

7. Если f интегрируема на (т.е. есть предел частичных сумм), то и модуль от нее интегрируем и справедлива формула

.

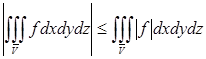8. Теорема о среднем: Если на и f – интегрируема, то , m- наименьшее значение, M- наибольшее по области , где - мера Жордано.

Следствия 8 свойства:

1.Обе части разделим на, получим , где .

2.Если кроме указанных условий теоремы о среднем функция непрерывна в любой точке области , то справедливо утверждение

,

где точка .

3. Если, то .

Вычисление тройного интеграла

1 случай. Область имеет следующий вид:

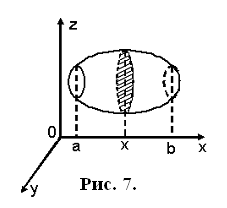
В данном случае считают, что - измеряемое сечение, функция определена на и интегрируема на нем. При таких условиях тройной интеграл будет определяться по формуле:

.

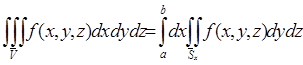Замечание: Считается, что - измеримая область с гладкой границей.

2 случай. Задана на непрерывная функция .

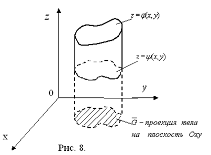
При таких условиях .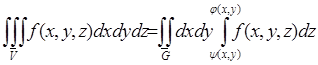

3 случай. Если область имеет специальный вид (дополнение ко второму случаю).

Структура допрофессионального образования в России
“Допрофессиональная подготовка - это первый этап в системе непрерывного образования и дополнительное образование к основному школьному”1. Допрофессиональное образование имеет целью профессиональную ориентацию учащихся и начальную подготовку работников квалифицированного труда по всем основным напра ...

Формы самостоятельной работы младших школьников на уроках литературного чтения во 2 классе
Большая часть времени на уроке отводится чтению и работе с текстом. Некоторые учителя считают, что многократным перечитыванием текста на уроке (сначала лучшими учениками, затем «цепочкой», по колонкам, разучивание текста хором и т.п.) можно добиться совершенствования навыков чтения первоклассников. ...

Характеристика других видов игровой деятельности дошкольника: строительные, подвижные, дидактические игры
Игровая деятельность детей не исчерпывается только сюжетно-ролевыми играми, хотя они наиболее характерны для дошкольника. Разновидностью сюжетно-ролевой игры являются строительные игры и игры-драматизации. Эту группу игр иногда называют творческими. В них дети не просто копируют те или иные стороны ...