Методические рекомендации по проведению лекционных занятий с применением информационных технологий

3.5 Разработка практического занятия

Практическое занятие №11

Тема: Тройной интеграл и его геометрические приложения

Тип занятия – практикум, форма занятия представляет собой комбинированную между коллективной и фронтальной.

Средствами обучения на данном практическом занятии являются: сборник задач по математическому анализу, рисунки на доске, методические рекомендации по проведению практических занятий.

При проведении занятия использовались следующие методы обучения – словесные, наглядные, по дидактической цели – познавательные, по характеру познавательной деятельности – проблемные.

Цель: при решении упражнений закрепить знания, умения и навыки, полученные на лекции в области вычисления тройных интегралов по любой области, с помощью замены переменных, вычисления объемов тел, координат центра тяжести.

Ход занятия:

I. Организационная часть

Студентам сообщается тема практического занятия, его цель, проводится проверка присутствующих.

II. Основная часть

В начале занятия проводится фронтальный опрос с целью проверки теоретических знаний по изученной теме. Студентам предлагается ответить на следующие вопросы у доски, выполняя необходимые при ответе записи (у доски работают 4 студента одновременно).

Вопрос 1. Сформулируйте определение тройного интеграла.

Ответ: Если при интегральная сумма

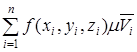
стремиться к конечному пределу, причем он не зависит от способа разбиения на подобласти и выбора точки , то функция называется интегрируемой по области , а сам предел называется тройным интегралом от функции по области и обозначается

.

Вопрос 2. Написать формулы вычисления тройного интеграла: для 1 и 2 случаев.

Ответ:

1.случай. Область имеет следующий вид:

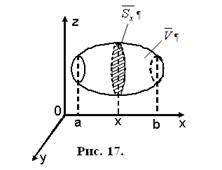
В данном случае считают, что - измеряемое сечение, функция определена на и интегрируема на нем. При таких условиях тройной интеграл будет определяться по формуле:

.

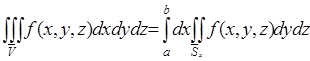Замечание: Считается, что - измеримая область с гладкой границей.

2 случай. Задана на непрерывная функция .

Принципы, цели и задачи эксперимента. Характеристика контингента
Диагностическая работа с детьми подчиняется основным законам диагностического исследования. Ребенок – это специфический объект исследования, его психика находится в стадии становления, развития, поэтому при ее изучении мы будем руководствоваться определенными принципами: Принцип гуманизма – любое и ...

Информационные ресурсы общества
Человечество развивается благодаря генерированию информации. Нет необходимости доказывать, что для человека информация такой же энергетический продукт, как и пища. Чтобы быть хозяином положения в своей сфере, избранной области знаний или бизнеса, необходимо быть в курсе научно-технических событий, ...

Функциональный аспект особенности использования речи учащимися с умеренной умственной отсталостью как регулятора поведения
В параграфе говорится об особенностях речи детей с умеренной умственной отсталостью при гидроцефалии, шизофрении, ревматизме либо травмах головного мозга и эпилепсии. Более сложной для детей с умеренной умственной отсталостью оказывается деятельность, контролируемая их собственными словесными обобщ ...