Методические рекомендации по проведению лекционных занятий с применением информационных технологий

Решение:

По формуле вычисления тройного интеграла (случай 3) имеем

.

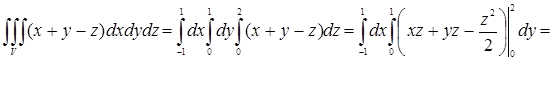
№2. (Студент с помощью преподавателя) Вычислить

,

где - пирамида, ограниченная плоскостью и координатными плоскостями , , [17].

Решение:

Для построения пирамиды найдем проекции на плоскости , , . На плоскость :,

На плоскость :,

На плоскость :,

Область проектируется на в треугольник , ограниченный прямыми , , .

По формуле вычисления тройного интеграла (случай 3) имеем

.

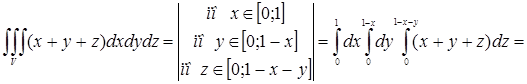
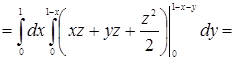
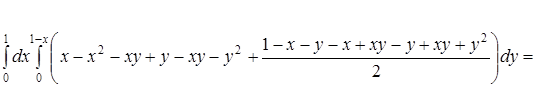
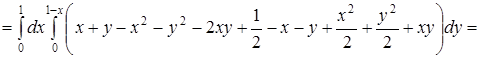
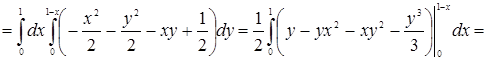
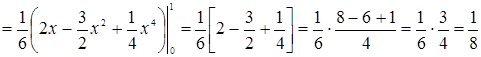№3. (Студент самостоятельно) Вычислить тройной интеграл

,

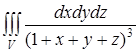где - пирамида, ограниченная плоскостью и координатными плоскостями, , [17].

Использование видео в старших классах
Кроме упражнений, где главную роль играет звуковая дорожка, на этом этапе можно использовать видео для изучения различных культурных и социокультурных явлений - видовые фильмы различной тематики для "опознания" культурно, значимых видов и памятников, портретов выдающихся деятелей прошлого ...

Особенности психического развития дошкольников подготовительной группы
Согласно «Программы воспитания и обучения в детском саду», под редакцией М.А. Васильевой, В.В. Гербовой, Т.С. Комаровой подготовительную группу детского сада посещают дети старшего дошкольного возраста. По концепции детства Д.Б. Эльконина детям этого возраста характерны потеря непосредственности и ...

Условия, обеспечивающие успешность самостоятельной работы
Самостоятельная работа, как работа по заданию, может успешно осуществляться только тогда, когда учащийся ясно осознает цель работы и у него есть стремление к достижению этой цели. Иными словами, успех самостоятельной работы обусловливается целенаправленностью учащихся. Кроме того, успех самостоятел ...