Методические рекомендации по проведению лекционных занятий с применением информационных технологий

Введем сферические координаты , , , .

Новые переменные изменяются в пределах , , .

Таким образом,

.

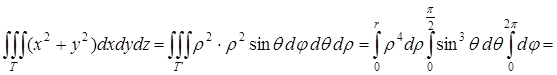
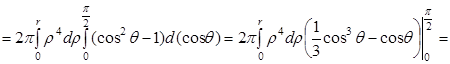
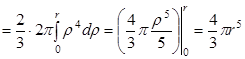№7(Преподаватель у доски) Вычислить объем тела, ограниченного сферой и параболоидом .

Решение:

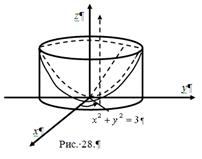
Найдем проекцию линии пересечения сферы и параболоида на плоскость . Для этого достаточно из системы уравнений , 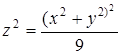исключить переменную . В результате получим: 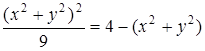или , откуда и - корни квадратного уравнения.

Следовательно, уравнением проекции будет окружность .

В силу симметрии достаточно вычислить объем тела находящегося в 1 октанте, и результат умножить на 4. Тогда согласно формуле: для искомого объема получим

Так как проекция данного тела на плоскость есть круг , то для вычисления последнего интеграла целесообразно перейти к цилинричиским координатам.

После преобразования по формулам: , , уравнения окружности , параболоида и сферы , соответственно принимают вид: , и . Из рисунка видно, что в области интегрирования угол изменяется от до , - от до , - от до . Поэтому

Понятие формы
Воспитательная работа, как любое социально-психологическое культурологическое явление, имеет форму. Форма воспитательной работы – это доступный внешнему восприятию образ взаимодействия детей с педагогом, сложившейся благодаря системе используемых средств, выстраиваемых в определенном логическом обе ...

Количественно-качественная характеристика результатов эксперимента
В ходе выполнения задания, составление рассказа по серии сюжетных картинок, дало возможность определить ряд специфических особенностей в проявлениях связной речи у детей с недоразвитием речи. Мною было выделено 3 уровня сформированности связной речи старших дошкольников с нормальным речевым развити ...

Методические рекомендации по проведению лекционных занятий с применением информационных технологий
Лекционный материал по теме «Тройные интегралы» приходится на конец 2-го курса и создает теоретическую основу для всех видов учебной деятельности по математическому анализу. К концу 2-го курса у студентов накапливается “критическая масса” опыта студенческой жизни, что позволяет ему окончательно пре ...