Методические рекомендации по проведению лекционных занятий с применением информационных технологий

Решение:

Найдем проекцию области на плоскость , то есть :, .

На плоскость :, .

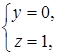
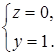На плоскость :, .

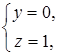
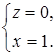Проекцией тела на плоскость служит треугольник , образованный прямыми , и .

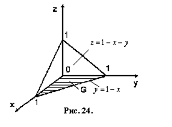
Границами изменения служат числа 0 и 1, а при постоянном переменная изменяется от 0 до .

Если же фиксированы и , и , то пределами изменения будут 0 и . По формуле

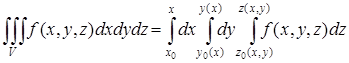получаем

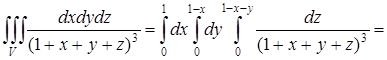
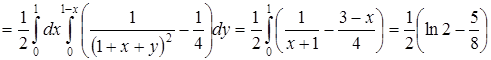[17].

Первичное закрепление материала проводится при решении студентами у доски упражнений, подобных рассмотренным. Остальные решают на месте, сверяя свое решение с решением у доски.

№4.(Преподаватель у доски) Вычислить тройной интеграл , если - шар [21].

Решение:

Перейдем к сферическим координатам , , , . В области координаты , , изменяются так: , ,

Особенности развития наглядно-образного мышления у старших дошкольников
В настоящее время, бесспорно, что чувственные образы, представления имеют существенное значение в умственном развитии ребенка. Вместе с тем в ряде исследований показано, что план представлений, план образного мышления недостаточно произволен, управляем даже у взрослых людей. Некоторые авторы пишут ...

Описание передового опыта по теме: «Формирование словаря у детей раннего возраста»
В нашем дошкольном учреждении работа по накоплению и уточнению активного и пассивного словарного запаса начинается с раннего возраста. Поставлены следующие задачи: 1. Научить детей слушать и понимать обращённую к ним речь и самим правильно пользоваться речью. 2. Формировать и обогащать словарь дете ...

Бессмертный подвиг двадцати восьми героев
Это было 16 ноября 1941 года. Фашисты рвались к Москве. Путь им преградили гвардейцы из дивизии генерала Панфилова. Их было 28 человек. Среди них были русские, казахи, украинцы. Прямо на них шли 20 фашистских танков. Отважные воины приняли неравный бой. Бой продолжался несколько часов. Враг двинул ...