Методические рекомендации по проведению лекционных занятий с применением информационных технологий

.

№5. Вычислить тройной интеграл , если область ограничена цилиндром и плоскостями , и [22].

Решение:

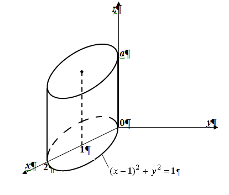
Перейдем к цилиндрическим координатам: , , , .

Уравнение цилиндра в этих координатах примет вид:

или , т.е. .

Следовательно, в области координаты , и изменяются так:

, , .

Поэтому

.

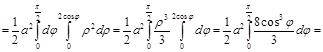
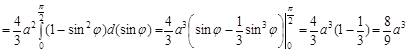Студент у доски, остальные работают самостоятельно, в конце решения сравнивают полученный результат

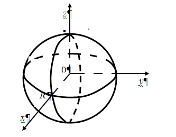
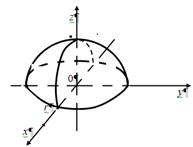
№6. Вычислить , если область - верхняя половина шара [17].

Решение:

Формирование умений младших школьников умений самостоятельно работать с текстом
Одним из важнейших требований современного обучения является вооружение учащихся умениями самостоятельно работать, учиться, способами действия, воспитание у них самостоятельности как черты личности. Современный подход к воспитанию квалифицированного читателя посредством формирования читательских ум ...

Сеть учреждений и служб, оказывающих социально-педагогическую, психологическую помощь
Сеть учреждений и служб, оказывающих социально-педагогическую помощь детям включает: o учреждения и службы образования (дошкольные, внешкольные, общеобразовательные школы, колледжи, лицеи, школы-интернаты, детские дома, ПТУ, средние профессиональные учебные заведения, вузы и др.), o учреждения и сл ...

Экспериментальное исследование развития музыкальности детей младшего дошкольного возраста в процессе восприятия музыки
В экспериментальном исследовании приняли участие 16 воспитанников младшей группы ДОУ при ОУ СОШ № 4 «Дошкольные группы» г.Сызрани Самарской области. Исследовательская работа проходила в три этапа: констатирующий, формирующий и контрольный. Цель опытно-экспериментальной работы: выявление начального ...