Методические рекомендации по проведению лекционных занятий с применением информационных технологий

.

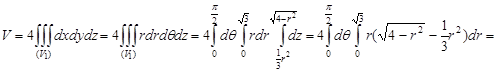
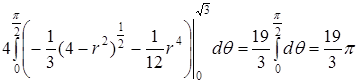Преподаватель: Итак, подведем итог: на сегодняшнем занятии мы с вами познакомились с тройным интегралом, вычислением его по любой области, научились вычислять тройной интеграл путем преобразования декартовых координат к цилиндрическим и сферическим координатам, находить объем тела. Для окончательного закрепления изученной темы на дом будут заданы аналогичные примеры.

Домашнее задание: сборник задач по математическому анализу для студентов второго курса факультета математики-информатики. Ниже приведены решенные номера домашнего задания.

Вычислить , где область определяется неравенствами , , .

Решение:

.

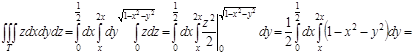
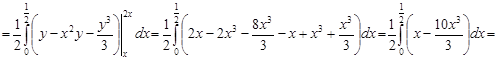
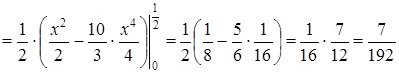№934. Вычислить интеграл , если область ограничена плоскостями ,, , .

Решение:

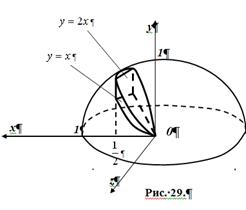
Область ограничена сверху плоскостью , а снизу плоскостью . Проекцией тела на плоскость служит треугольник, образованный прямыми , , .

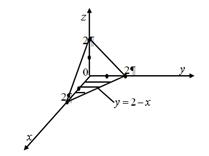
Следовательно, по формуле вычисления тройного интеграла

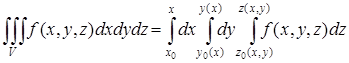
получаем

.

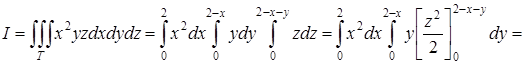
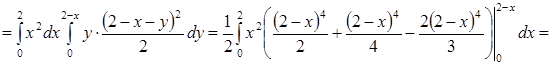
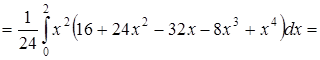
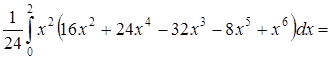
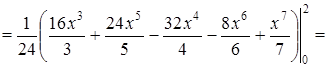
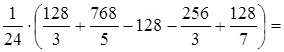
№949. Вычислить , где область - шар .

Задачи воспитания в семье
Развитие интеллекта и творческих способностей, познавательных сил и первичного опыта трудовой деятельности, нравственное и эстетическое формирование, эмоциональная культура и физическое здоровье детей – все это зависит от семьи, от родителей, и все это составляет задачи семейного воспитания. В перв ...

Преобразование пространств и криволинейные координаты
Идеи, развитые в связи с преобразованием плоских областей, естественно переносятся и на случай пространственных областей. Пусть имеем пространство, отнесенное к системе прямоугольных координат , и другое пространство с системой координат . Рассмотрим две замкнутые области и в этих пространствах огр ...

Основные функции деятельности классного руководителя и способы его общения с родителями
Классный руководитель - это педагог-профессионал, являющийся для растущего человека духовным посредником между обществом и ребенком в усвоении основ человеческой культуры; защитником от моральной деградации, нравственной гибели; организатором отношений сотрудничества в разнообразных видах совместно ...