Преобразование пространств и криволинейные координаты

Впрочем, все это будет так лишь в предположении строгой однозначности соответствия между областями и . На практике эта однозначность часто нарушается.

1) Цилиндрические координаты представляют соединение полярных координат в плоскости с обычной декартовой аппликатой . Формулы, связывающие их с декартовыми, имеют вид

, ,

Эти формулы отображают область

, ,

на все пространство . Отметим, однако, что прямая , отображается в одну точку ; этим нарушается взаимная однозначность соответствия.

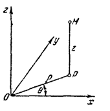
Рис. 4.

Координатные поверхности в рассматриваемом случае будут:

а)— цилиндрические поверхности с образующими, параллельными оси ; направляющими для них служат окружности на плоскости с центром в начале;

б) — полуплоскости, проходящие через ось ;

в) — плоскости, параллельные плоскости .

Якобиан преобразования:

.

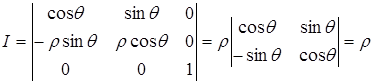Исключая случай , якобиан сохраняет положительный знак.

2) Сферические координаты, называемые иначе полярными координатами в пространстве, связаны с декартовыми формулами:

, , ,

Где , , .

Геометрический смысл величин , , ясен из puc.5: есть радиус вектор , соединяющий начало(полюс) с данной точкой ;— угол, составляемый с осью координат (полярной осью); - угол, составляемый с осью проекцией (перпендикулярную к полярной оси).

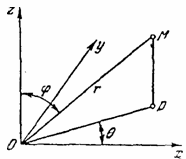
Рис.5.

В этом случае снова сталкиваемся с нарушением взаимной однозначности соответствия: плоскость пространства отображается в начало координат , прямая , отображается в одну точку , .

Анализ и сравнение познавательного интереса младших школьников с традиционной и вальдорофской системами обучения
вальдорфский обучение познавательный интерес По данным методики Г.Н.Казанцевой были установлены следующие результаты: Раздел I. Любимые предметы 3б 3в 1.Физкультура (22ответа) 2.ИЗО (16 ответов) 3. Математика (14 ответов) 1. Математика (12 ответов) 2. Физкультура (10 ответов) 3. Окружающий мир (8 о ...

Содержание воспитания как основное средство реализации воспитания
Один из наиболее спорных вопросов - содержание воспитания. Известно, что цель воспитания - всестороннее гармоническое развитие личности. Термин всестороннее воспитание предполагает конкретную дифференциацию его на составляющие: умственное, нравственное, трудовое, эстетическое, физическое и т.д. Все ...

Формы и содержание работы с семьей
Целью социально-педагогической деятельности является реализация программы комплексной поддержки. Организация социально-педагогической работы осуществляется поэтапно. На начальном этапе происходит диагностика микросоциума и воспитательного потенциала семьи. Сюда относятся материальные и бытовые усло ...