Преобразование пространств и криволинейные координаты

Идеи, развитые в связи с преобразованием плоских областей, естественно переносятся и на случай пространственных областей.

Пусть имеем пространство, отнесенное к системе прямоугольных координат , и другое пространство с системой координат . Рассмотрим две замкнутые области и в этих пространствах ограниченные соответственно поверхностями и , которые всегда будем предполагать кусочно-гладкими. Допустим, что эти области связаны между собой взаимно однозначным непрерывным соответствием, которое осуществляется формулами:

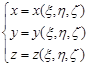
При этом, необходимо, точкам поверхности отвечают именно точки поверхности , и наоборот.

Пусть функции (19) имеют в области непрерывные частные производные; тогда и якобиан

также является непрерывной функцией в . Здесь будем считать, что этот определитель всегда отличен от нуля, сохраняя определенный знак.

Если в области взять кусочно- гладкую поверхность:

, ,

(предполагая, что параметры изменяются в некоторой области на плоскости ), то формулы (19) преобразуют ее в кусочно-гладкую же поверхность в области . Эта поверхность будет иметь уравнения

.

Ограничимся случаем гладкой поверхности: на ней особых точек нет, так что определяем:

, ,

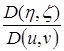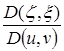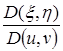
одновременно в нуль не обращаются. Проверке подлежит лишь отсутствие особых точек и на поверхности.

Имеем линейные равенства относительно величин:

,

,

.

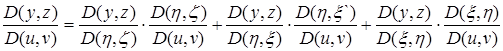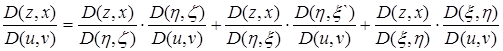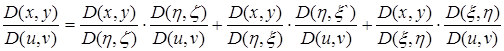Определитель, составленный из коэффициентов при этих величинах, т.e. из алгебраических дополнений к элементам определителя , по известной теореме алгебры равен квадрату этого последнего и, следовательно, вместе с ним отличен от нуля. Если бы левые части написанных равенств в какой-нибудь точке одновременно обратились а нуль, то нулями были бы и все три определителя, что противоречило бы допущению.

Числа , , однозначно характеризующие положение точки в пространстве , называются криволинейными координатами этой точки. Точки пространства , для которых одна из этих координат сохраняет постоянное значение, образуют координатную поверхность. Всего будет существовать три семейства таких координатных поверхностей; через каждую точку области проходит по одной поверхности каждого семейства.

Примерная модель формирования научного мировоззрения в процессе образования и воспитания
Понятие "мировоззрение" можно определить следующим образом - это система философских, научных, социально-политических, нравственных, эстетических взглядов и убеждений человека, которые отражают в его сознании общую картину мира и определяют направленность его деятельности. Как правило, вы ...

Виды и структура дидактических игр
формирование словарь дидактический игра В дошкольной педагогике все дидактические игры можно разделить на три основных вида: игры с предметами ( игрушками, природным материалом), настольно-печатные и словесные игры. С детьми раннего возраста используются дидактические игры с игрушками и картинками, ...

Развитие процессов мышления и понимания в рамках культурно исторической концепции
Концепция разрабатывалась Выготским и его школой (Леонтьев, Лурия и др.) в 20-30 гг. XX в. Одной из первых публикаций была статья "Проблема культурного развития ребенка" в журнале "Педология" в 1928 г. Следуя идее общественно-исторической природы психики, Выготский совершает пер ...