Преобразование пространств и криволинейные координаты

Координатные поверхности составляют три семейства:

а) — концентрические сферы с центром в начале координат;

б) — круговые конусы, осью которых служит ось ;

в) — полуплоскости, проходящие через ось .

Якобиан этого преобразования:

.

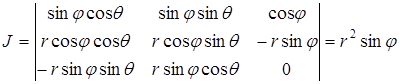Якобиан сохраняет знак плюс, за исключением упомянутых выше случаев, когда , либо , и якобиан обращается в нуль.

3) Преобразование пространства самого в себя по формулам:

, ,

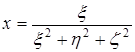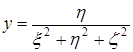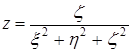
однозначно обратимо:

, , .

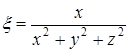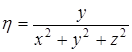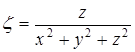Оно называется инверсией.

4) Эллиптические координаты. Рассмотрим семейство софокусных и соосновных поверхностей второго порядка:

,

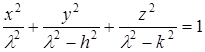
состоящее из эллипсоидов (при ), однополостных гиперболоидов (при ) и, наконец, двуполостных гиперболоидов (при ).

Через каждую точку пространства, не лежащую на координатах плоскостях, проходит по одной поверхности каждого типа. Действительно, левая часть уравнения, получаемого из :

,

имеет знак минус при , знак плюс при , снова знак минус при и, наконец, знак плюс при больших . Отсюда следует, что уравнение имеет три положительных корня: один (что отвечает эллипсоиду), второй , (он дает однополостный гиперболоид), третий (двуполостной гиперболоид).

Используя свойства корней написанного выше уравнения, которое мы можем рассматривать как кубическое уравнение относительно , а именно:

,

;

,

найдем:

, ,

.

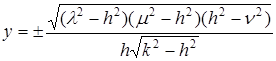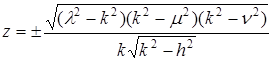Если ограничиться первым координатным октантом, то в этих формулах надлежит сохранить лишь положительные знаки. Числа можно рассматривать, как криволинейные координаты точек этого угла. Их и называют эллиптическими координатами. Три семейства координатных поверхностей - это и будут семейства эллипсоидов, однополостных и двуполостных гиперболоидов, о которых была речь выше.

Якобиан преобразования имеет вид:

Формы и содержание работы с семьей
Целью социально-педагогической деятельности является реализация программы комплексной поддержки. Организация социально-педагогической работы осуществляется поэтапно. На начальном этапе происходит диагностика микросоциума и воспитательного потенциала семьи. Сюда относятся материальные и бытовые усло ...

Проблемы организация самостоятельной работы и ее задачи
Начальное обучение является фундаментом образования. От того, насколько прочно заложены основы первоначального обучения, зависит дальнейшее формирование знаний и умений в средних классах школы. И не только содержание обучения в начальных классах является подготовительным курсом к основам наук, вся ...

Содержание воспитания как основное средство реализации воспитания
Один из наиболее спорных вопросов - содержание воспитания. Известно, что цель воспитания - всестороннее гармоническое развитие личности. Термин всестороннее воспитание предполагает конкретную дифференциацию его на составляющие: умственное, нравственное, трудовое, эстетическое, физическое и т.д. Все ...