Замена переменных в тройных интегралах

С помощью выражения объема в криволинейных координатах нетрудно установить и общую формулу замены переменных в тройных интегралах.

Пуста между областями и пространств и cyществует соответствие, охарактеризованное в п0 2.1. Считая соблюденными все условия, при которых была выведена формула (26), покажем теперь, что имеет место следующее равенство

где 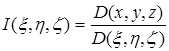, вполне похожее формуле замены переменных в двойных интегралах. При этом функцию предполагаем непрерывной или, самое большее, допускающей разрывы вдоль конечного числа кусочно-гладких поверхностей (но во всяком случае сохраняющей ограниченность). Таким образом, существование обоих интегралов в равенстве не вызывает сомнений; нужно установить лишь самое равенство.

Разложив кусочно-гладкими поверхностями области и на (соответствующие друг другу) элементарные части и , применим к каждой паре областей , формулу (25); получим

,

где есть некоторая точка области не зависящая от выбора. Возьмем соответствующую точку области , т. е. положим

, , ,

и составим интегральную сумму для первого из интегралов:

.

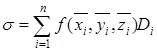Подставив сюда вместо , , выражения , а вместо —выражение (28), придем к сумме

,

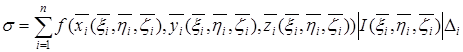которая, очевидно, уже является интегральной суммой для второго из интегралов .

Устремим к нулю диаметры областей , вследствие чего в силу непрерывности соответствия устремятся к нулю и диаметры областей . Сумма должна стремиться одновременно к обоим интегралам, откуда и следует требуемое равенство.

Как и в случае двойных интегралов формула имеет место и при нарушении сформулированных выше при доказательстве формулы предположений в отдельных точках или вдоль конечного числа кусочно-гладких линий и поверхностей, лишь бы якобиан сохранял ограниченность.

Можно пойти дальше при расширении условий применимости формулы (28), допуская и несобственные интегралы. Подчеркнем еще раз, что при указанных там условиях формула имеет место в предположении существования одного из интегралов , существование другого отсюда уже будет вытекать.

Методы и приёмы словарной работы
Можно выделить две группы методов: методы накопления содержания детской речи ( методы ознакомления с окружающим миром и обогащения словаря) и методы, направленные на закрепление и активизацию словаря, развитие его смысловой стороны. Методы накопления содержания детской речи: 1. Рассматривание предм ...

Содержание работы социального педагога в образовательном учреждении
социальный школа педагог семья Содержание работы социального педагога в соответствии с квалификационной характеристикой определяется ее педагогической направленностью. Это означает, что вся его профессиональная деятельность, по сути, представляет собой комплекс мероприятий по воспитанию, образовани ...

Пьезоэлектрические свойства полимеров
Пьезоэлектричеством называется генерирование диэлектриками электрических зарядов при их механической деформации (нагружении) или механическая деформация диэлектриков при приложении внешнего электрического поля. Использование полимеров в качестве пьезоэлектриков в настоящее время широко распростране ...