Описание предметных линий в диагностических материалах

Интерпретация данных

При решении учениками задач на разном материале мы выдели, что испытуемые, решающие задания третьего уровня

а) выделяют структуру задач,

б) выделяют законы перевода одного знакового плана в другой.

К сожалению, часть гипотезы о том, что опосредствование действия моделирования задач третьего уровня включает интонационное воссоздание переходов от одного знакового плана к другому, мы придумали поздно, поэтому интонационной информации у нас нет. Но есть данные о взаимосоотнесении различных знаковых планов и выделения структуры задач. Поэтому в целом может сказать, что наша гипотеза подтвердилась.

Протокол эксперимента на примере задач с полосками

Задание 1. (задание первого уровня)

Петр склеивает из одинаковых полосок разные фигуры.

Длина каждой полоски – 7 см, а ширина – 2 см.

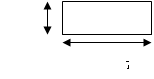Вопрос 1. Какова площадь поверхности одной полоски (сколько квадратов со стороной 1 см помещается на поверхности полоски)?

Обведи правильный ответ.

А. 9 В. 11 Г. 14 Д. 15

Дает ответ 14 – вариант Г

Задание 2. (задание второго уровня)

Петр склеил фигуру из двух пересекающихся полосок.

Какова площадь полученной фигуры, если длина каждой полоски 7 см, а ширина 2 см?

Обведи правильный ответ.

А. (7 х 2) + (7 х 2) = 28

Б. 2 х 2 х 5 = 20

В. 7 х 2 х 2 – 4 = 24

Г. (7 + 2) х 2 + 7 = 25

Дает ответ 28 - А. Испытуемый не делает сопоставления двух знаковых планов: наглядно-образного плана и математической модели.

Я ввожу опосредствование. Изменяю структуру задачи, а именно меняю наглядно-образный план. Даю задачу: «Даны две другие полоски:

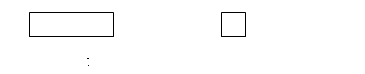
Меньшую полоску наклеили на большую вот так:

Какой периметр будет у полученной полоски?»

Испытуемый принимает данное опосредствование, он решает эту задачу - дает ответ 14.

Потом смотрит на задание и дает ответ В. Задача решена. Испытуемый дает правильную интерпретацию всех данных и действий в решении: «7*2 – площадь одной полоски. На рисунке 2 одинаковые полоски, поэтому их площадь умножили на 2 и вычли площадь фигуры на их пересечении».

Эти задачи мы давали с целью овладения учеником материалом, на котором будет построена задача третьего уровня.

Задание 3.

Петр рассчитал площадь полоски, склеенной из двух других.

Вот его расчет:

(7 + 3) х 2 = 20

Какую из приведенных ниже полос он имел в виду?

Обведи правильный ответ.

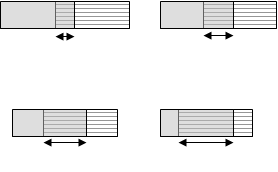А Б

2 3

В Г

4 5

Задание 3 мы показываем ученику, но не даем решать.

Задание 4. (задание третьего уровня)

Петр задумал склеить одну полосу определенной длины из трех других. Чтобы намазать клеем квадрат со стороной 1 см, нужен 1 грамм клея.

Петр рассчитал, что ему для этого понадобится 12 граммов клея:

3 х 2 + 3 х 2 = 12

Чтобы склеить между собой две поверхности, клей надо намазать только на одну из них.

Какой длины полоса получится у Петра?

Решение:

Ученик уточняет, как построен наглядно-образный план задачи. Он задает вопрос: «Как склеены полоски?» Я спрашиваю, как бы он склеивал одинаковые полоски, чтобы получить одну более длинную? Я обращаю его внимание на рисунки из задания 3. Он уточняет у меня, что полоски в задании 3 такие же, как и в предыдущих заданиях. Вычисляет все недостающие моменты длины для полоски В из задания 3:

Характеристика практических методов обучения
В процессе обучения большое значение имеет выра­ботка у учащихся умений и навыков применения полученных знаний на практике. Метод упражнений. Умения и навыки формируются с помощью метода упражнений. Сущность этого метода состоит в том, что учащиеся производят многократные действия, т.е. тренируются ...

Изучение особенностей грамматического строя речи у нормально развивающихся детей и у детей с трудностями в обучении
На данном этапе работы ставились следующие задачи: - выявить механизм аграмматизма в грамматическом оформлении высказываний у учащихся в норме и при патологии; - определить принципы и методы обучения в формировании грамматического строя речи и апробировать их на уроках и коррекционных занятиях; - о ...

Методические рекомендации по формированию связной речи детей старшего дошкольного возраста с общим недоразвитием речи в процессе рассказывания по сюжетной картинке
речь логопедический дошкольник принцип Методические рекомендации разработаны с учетом работ следующих авторов: Т.Б. Филичевой, Г.В. Чиркиной, В.И. Селиверстова и др., а также с учетом программы Филичевой Т.Б., Чиркиной Г.В. "Подготовка к школе детей с общим недоразвитием речи в условиях специа ...