Несобственные тройные интегралы

где расстояние элемента (или точки, в которой мы считаем сосредоточенной его массу) от точки . Суммируя, для проекций полной силы притяжения на оси координат получим

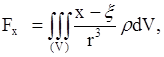
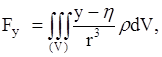
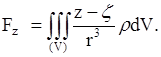
Аналогично определяется и потенциал нашего тела на точку:

.

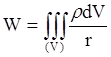Если точка лежит вне тела, то все эти интегралы оказываются собственными. В этом случае можно дифференцировать интеграл по любой из переменных , , под знаком интеграла на основании соображений, сходных с теми, которыми пользовались в отношении простых интегралов. В результате мы и получим, что

, ,

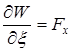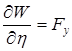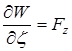
В случае же, когда точка сама принадлежит телу , в этой точке , и подинтегральные функции в и вблизи нее перестают быть ограниченными.

Выбор музыкального произведения для беседы
«Щелкунчик» — соч. 71, балет Петра Ильича Чайковского в двух актах на либретто Мариуса Петипа по мотивам сказки Эрнеста Гофмана «Щелкунчик и мышиный король». Щелкунчик - это добрый друг и старый знакомый, который не раз приходил к нам в гости, и ещё много раз придёт… И каждый знает своего собственн ...

Организация личностно-ориентированного обучения в процессе обучения дизайну
Образовательный процесс строится на учебном диалоге ученика и учителя, который направлен на совместное конструирование программной деятельности. В любом учебном предмете, в особенности в изобразительном искусстве, где, кроме прочего, важен талант и эстетический вкус, уже заложенные генетически, уче ...

Проблемы коммуникативной сферы учащихся коррекционных образовательных учреждениях VIII вида
Для социальной адаптации человека очень важно его общение с другими людьми, умение вступить в беседу и поддержать ее, т.е. необходим определенный уровень сформированности диалогической речи. Ученики младших классов редко бывают инициаторами диалога. Это связано с недоразвитием их речи, с узким круг ...