Несобственные тройные интегралы

В случаях, когда область интегрирования простирается в бесконечность или подинтегральная функция перестает быть ограниченной вблизи особых точек, линий или поверхностей, несобственный тройной интеграл получается помощью дополнительного предельного перехода, исходя из собственного интеграла.

Несобственные тройные интегралы также являются необходимо абсолютно сходящимися. Это обстоятельство сводит весь вопрос о существовании и вычислении таких интегралов к случаю положительной (неотрицательной) подинтегральной функции.

Естественно, что все геометрические и механические величины, связанные с распределением масс в пределах некоторого тела в пространстве, в принципе выражаются на этот раз тройными интегралами, распространенными на тело .Здесь также проще всего пользоваться принципом "суммирования бесконечно малых элементов".

Обозначим через плотность распределения масс в произвольной точке тела ; она является функцией от координат точки; эту функцию мы будем всегда предполагать непрерывной. Суммируя элементы массы , для величины всей массы будем иметь

Исходя из элементарных статических моментов

, ,

найдем самые статические моменты:

, , ,

а по ним —и координаты центра тяжести:

, , .

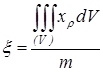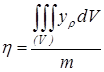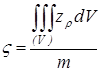В случае однородного тела, , получаем проще:

, , .

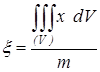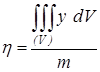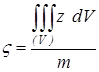Сами собой понятны и формулы для моментов инерции относительно осей координат:

, ,

или относительно координатных плоскостей:

,, .

Наконец, пусть массы, заполняющие тело , оказывают притяжение на точку (массы 1) по закону Ньютона. Сила притяжения со стороны элемента массы имеет на оси координат проекции

Содержание работы по повышению уровня гуманистических качеств среди старшеклассников
II этап Формирующий, который проходил с ноября 2009 по декабрь 2009 г. Цель формирующего эксперимента – провести коррекцию уровня гуманистических качеств в позитивную сторону. Задачи формирующего эксперимента: - разработать программу Тренинга «Гуманистическое отношение к жизни»; - провести в период ...

Изучение школьников в целях профориентации
Изучение учащихся в целях профориентации (предварительная профдиагностика), как уже было сказано выше, составляет один из важнейших составных компонентов профориентации школьников. На этом этапе следует изучить характерные особенности личности: ценностные ориентации, интересы, потребности, склоннос ...

Общая характеристика существующих методов обучения учащихся с умеренной умственной отсталостью
В данном параграфе раскрываются понятия «образование», «обучение», «воспитание», «коррекционное обучение», «коррекционное воспитание» и «коррекционное развитие», также рассматриваются методы формирования вербальных средств общения в ситуации делового взаимодействия и методы коммуникативного подхода ...