Свойства интегрируемых функций и тройных интегралов

1. Существование и величина тройного интеграла не зависят от значений, принимаемых функцией вдоль конечного числа поверхностей с объемом 0.

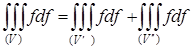2. Если , то , причем из существования интеграла слева вытекает уже существование интегралов справа, и обратно.

3. Если k= const, топричем из существования интеграла справа следует существование интеграла слева.

4. Если в области (V) интегрируемы две функции f и g, то интегрируема и функция , причем

5. Если для интегрируемых в области (V) функции, f и g выполняется неравенство , то

6. В случае интегрируемости функции интегрируема и функция , и имеет место неравенство

.

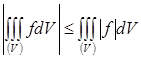7. Если интегрируемая в функция удовлетворяет неравенству , то

Иными словами, имеет место теорема о среднем значении

.

В случае непрерывности функции эту формулу можно написать

где есть некоторая точка области .

Устанавливаем понятие функции от (трехмерной) области, в частности, аддитивной функции.

Важным примером такой функции является интеграл по переменной области :

Вводится аналогично прежнему понятие производной функции по области в данной точке , так называется предел

при стягивании к точке М содержащей ее области .

8. Если подинтегральная функция непрерывна, то производная

Рис. 1.

по области в точке от интеграла (4) будет равна значению подинтегральной функции в этой точке, т. е.

Таким образом, при сделанном предположении интеграл (4) служит для функции в некотором смысле «первообразной» и, как доказывается аналогично плоскому случаю, единственной аддитивной первообразной.

Цели и задачи обучения английскому языку на профильном уровне. Требования к уровню подготовки выпускников
Изучение иностранного языка в целом и английского языка, в частности, на профильном уровне в старшей школе направлено на достижение следующих целей: • Дальнейшее развитие иноязычной коммуникативной компетенции (речевой, языковой, социокультурной, компенсаторной и учебно-познавательной): речевая ком ...

Особенности профильного обучения в средних общеобразовательных учреждениях
В русле модернизации образования в новых программах по ИЯ вводится предпрофильная подготовка в девятых классах и профильное обучение в десятых-одиннадцатых классах средней школы. Целью профильного обучения является углубленная подготовка старшеклассников к постоянно усложняющимся требованиям соврем ...

Сущность понятия «музыкальная выразительность исполнения»
Музыка, как и каждый из видов искусства, имеет свои особенности, свои условности, свои специфические черты. Вместе с тем, музыке неотъемлемо присущи качества, объединяющие ее с другими искусствами; говоря иными словами, музыка подчиняется общим законам искусства. Основным из этих законов является т ...