Тройной интеграл и условия его существования

При построении общего определения нового интегрального образования тройного интеграла - основную роль играет понятие объема тела.

С понятием объема уже знакомы. Условие существования объема для данного тела заключается в том, чтобы ограничивающая его поверхность имела объем 0 . Только такие поверхности будем рассматривать, так, что существование объемов во всех нужных нам случаях тем самым обеспечивается. В частности, в состав указанного класса поверхностей входят кусочно-гладкие поверхности.

Пусть теперь в некоторой пространственной области (V) задана функция f(x, y, z). Разобьем эту область с помощью сети поверхностей на конечное число частей (V1), (V2), … , (Vn), имеющих соответственно объемы V1, V2, … ,Vn. В пределах i-го элемента возьмем произвольную точку , значение функции в этой точке умножим на объем Vi и составим интегральную сумму

Vi.

Конечный предел I этой суммы, при стремлении к нулю наибольшего из диаметров всех областей (Vi) и называется тройным интегралом функции f(x, y, z) в области (V). Он обозначается символом

.

Конечный предел подобного вида может существовать только для ограниченной функции. Для такой функции вводятся, кроме интегральной суммы σ, еще суммы Дарбу:

, ,

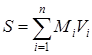где , .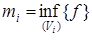

Обычным путем устанавливается, что для существования интеграла необходимо и достаточно условие

или ,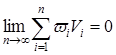

где есть колебание функции f в области . Заметим, что при существовании интеграла обе суммы s, S также имеют его своим пределом.

Отсюда непосредственно следует, что всякая непрерывная функция f интегрируема.

Можно несколько расширить эти условия, а именно: интегрируема всякая ограниченная функция, все разрывы которой лежат на конечном числе поверхностей с объемом 0.

Доказательство этого утверждения основано на следующей лемме:

Если область (V), содержащая поверхность (S) с объемом 0, разложена на элементарные области, то сумма объемов тех из них, которые задевают поверхность (S), стремиться к нулю вместе с диаметрами всех частичных областей.

Разработка занятия в 3-м классе на тему «Лес – природное сообщество» с использованием сюжетно-ролевой игры
Актуальность экологического воспитания сегодня имеет большое значение. Очень важно уже в детстве сформировать у ребенка щадящее, оберегающее и ответственное отношение как к ресурсам и объектам дикой природы, так и к достижениям цивилизации, этой «второй» природы, созданной руками и умом человека. Ч ...

Выявление уровня сформированности гуманизма у старшеклассников
I этап (констатирующий эксперимент) выявление уровня сформированности гуманизма у старшеклассников, который проходил в октябре-ноябре 2009 г. Опытно-экспериментальная работа была проведена на базе МОУ № 64 г. Тольятти. В исследовании принимали участие дети старшего школьного возраста –11 «А» (25 че ...

Контроль, его виды и функции. Нетрадиционные формы контроля экстенсивного чтения
элективные курсы английский обучение Проблема контроля в обучении иностранным языкам по-прежнему остается одной из наиболее актуальных в методике, а что касается осуществления контроля экстенсивного чтения у студентов, то этот аспект вообще довольно слабо освещен в методике. Существует несколько по ...