Выражение объема в криволинейных координатах

Возвращаясь к предположениям и обозначениям п° 1.1, поставим себе задачей выразить объем (ограниченного) тела в пространстве . Иным интегралом, распространенным на соответствующее тело в пространстве .

Искомый объем выражается, прежде всего поверхностным интегралом второго типа:,распространенным на внешнюю сторону поверхности . Отсюда постараемся перейти к обыкновенному двойному интегралу.

Будем исходить из параметрических уравнений поверхности ( изменяются в области на плоскости ). Тогда уравнения выразят, очевидно, поверхность .

Полагая 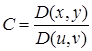, имеем:.

При этом интеграл берется со знаком плюс, если ориентация поверхности , связанная с рассмотрением внешней ее стороны соответствует ориентации плоскости , что всегда можно предположить.

Так как зависят от через посредство переменных , то, по известному свойствy функциональных определителей:

.

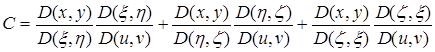Подставляя выражение в полученный выше интеграл, найдем:

.

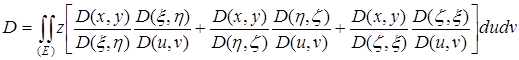Сопоставим этот интеграл с поверхностным интегралом второго типа, распространенным на внешнюю сторону поверхности :

.

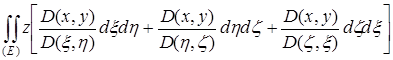Если его преобразовать, исходя из параметрических уравнений к обыкновенному двойному интегралу придем как раз к интегралу. Единственное различие между этими интегралами может заключаться лишь в знаке: если ориентация плоскости соответствует ориентации поверхности , связанной с рассмотрением внешней ее стороны, то интегралы равны, в противном же случае они разнятся знаками.

Наконец, от интеграла по формуле Остроградского можно перейти к тройному интегралу по области :

.

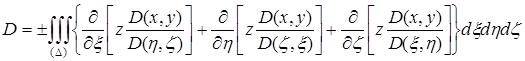Подинтегральное выражение равно:

Сумма, стоящая здесь в первой строке, равна якобиану:

,

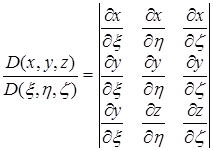в чем легко убедиться, разлагая этот определитель по элементам последней строки; сумма же в квадратных скобках, как показывает непосредственное вычисление, равна нулю. Таким образом, приходим к формуле:

.

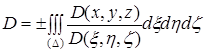Если вспомнить, что по предположению якобиан сохраняет знак, который он сообщает и интегралу, то станет ясно (так как здесь считаем ), что знак перед интегралом должен совпасть со знаком якобиана. Это дает нам право переписать полученный результат в окончательной форме:

Методы и формы организации эстетического воспитания дошкольников
Каждой группе задач эстетического воспитания соответствуют свои методы. Как говорилось выше, первая группа задач направлена на приобщение детей к искусству, развитие у дошкольников эстетического вкуса, понимание прекрасного. Ведущими методами для решения этих задач являются: показ, наблюдение, объя ...

Пути развития фонематического слуха у детей старшего дошкольного возраста
Основной целью логопедического воздействия при дислалии является формирование умений и навыков правильного воспроизведения звуков речи. Чтобы правильно воспроизводить звуки речи (фонемы), ребенок должен уметь: - узнавать звуки речи и не смешивать их в восприятии (т.е. узнавать звук по акустическим ...

Психолого-педагогические особенности деятельности специалиста по социальной работе с семьёй
Говоря о практике социальной работы с семьей, нельзя оставить без внимания психолого-педагогические особенности деятельности специалиста в работе с семьёй. К сожалению, в сложившейся ситуации социальный педагог работает с проблемными, социально-незащищёнными семьями, а для этого ему необходимо влад ...