Вычисление тройного интеграла, распространенного на параллелепипед

Изложение вопроса о вычислении тройного интеграла начнем с того случая, когда тело, в котором определена функция , представляет собой прямоугольный параллелепипед (рис.1), проектирующийся на плоскость в прямоугольник .

Теорема. Если для функции существует тройной интеграл

(5)

и при каждом постоянном из — двойной интеграл

,

то существует также повторный интеграл

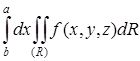, (7)

и выполняется равенство

.

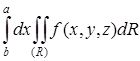доказательство: Разделим промежутки , , на части с помощью точек

,

,

,

тем самым разложим параллелепипед (Т) на элементарные параллелепипеды

и одновременно прямоугольник — на элементарные прямоугольники

(где и пробегают те же значения, что и только что).

Положив

имеем в силу 1.3, 1.7,

для всех значений из . Фиксируя произвольное значение , в этом промежутке, просуммируем подобные неравенства для всех значений j и k; мы получим неравенства

.

Наконец, умножим эти неравенства почленно на и просуммируем на этот раз по значку :

.

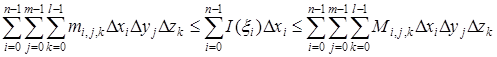Крайние члены представляют собой суммы Дарбу для интеграла и стремятся к нему, как к пределу, при стремлении к нулю всех разностей , , . Значит, к тому же пределу стремится интегральная сумма, стоящая посредине. Этим доказано одновременно как существование интеграла, так и равенство. Если предположить еще существование простого интеграла

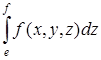
при любых значениях х из , у из ,то двойной интеграл в равенстве (8) можно заменить повторным и окончательно получим:

.

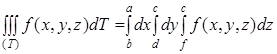Таким образом, вычисление тройного интеграла приводится к последовательному вычислению трех простых интегралов. Роли переменных , в формуле (10), разумеется, могут быть произвольно переставлены.

Если , то

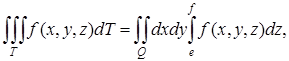
И здесь роли переменных можно переставлять.

В частности, для случая непрерывной функции ,очевидно, имеют место все формулы (8), (10), (11) и им подобные, получающиеся перестановкой переменных [3].

Современные формы и методы работы педагога по формированию ЗОЖ
«Здоровье формирующие образовательные технологии», по определению Н.К. Смирнова, - это все те психолого-педагогические технологии, программы, методы, которые направлены на воспитание у учащихся культуры здоровья, личностных качеств, способствующих его сохранению и укреплению, формирование представл ...

Цели и задачи воспитания у дошкольников экологической культуры
Создание нового отношения человека к природе — задача не только социально-экономическая и техническая, но и нравственная. Она вытекает из необходимости воспитывать экологическую культуру, формировать новое отношение к природе, основанное на неразрывной связи человека с природой. Одним из средств ре ...

Средства и методы воспитания
В широком смысле слова под средствами воспитания понимают способы организованного и неорганизованного воздействия, при помощи которых одни люди (воспитатели) воздействуют на других людей (воспитанников) с целью выработать у них определенные психологические качества и формы поведения. Под психологич ...