Задача о вычислении массы тела

Пусть дано некоторое тело (V), заполненное массами, и в каждой его точке M(x, y, z) известна плотность распределение ρ = ρ(M)=ρ(x, y, z) этих масс. Требуется определить всю массу m тела.

Для решения этой задачи разложим тело (V) на ряд частей: (V1), (V2), … , (Vn) и выберем в пределах каждой из них по точке .

Примем приближенно, что в пределах части (Vi) плотность постоянна и равна как раз плотности в выбранной точке. Тогда масса этой части приближенно выразится так:

,

масса же всего тела будет

.

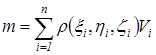Если диаметры всех частей стремятся к нулю, то в пределе это приближенное равенство становиться точным, так что

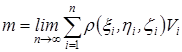, (1)

и задача решена.

Видно, что решение задачи и здесь привело к рассмотрению предела своеобразной суммы - типа интегральных сумм различного вида.

Подобного рода интегральные суммы приходится часто рассматривать в механике и в физике; они получили название тройных интегралов. В принятых обозначениях полученный выше результат запишется так:

(2)

Понятие формы
Воспитательная работа, как любое социально-психологическое культурологическое явление, имеет форму. Форма воспитательной работы – это доступный внешнему восприятию образ взаимодействия детей с педагогом, сложившейся благодаря системе используемых средств, выстраиваемых в определенном логическом обе ...

Содержание работы социального педагога в образовательном учреждении
социальный школа педагог семья Содержание работы социального педагога в соответствии с квалификационной характеристикой определяется ее педагогической направленностью. Это означает, что вся его профессиональная деятельность, по сути, представляет собой комплекс мероприятий по воспитанию, образовани ...

Психология восприятия картинки в раннем возрасте
Как уже отмечалось, познание начинается с ощущений и восприятий окружающих предметов, образы которых сохраняются в представлении и памяти. Оно происходит в процессе активного взаимодействия ребёнка с действительностью, в процессе так называемых практических проб, которые позволяют ему лучше познако ...