Вычисление тройного интеграла по любой области

Общий случаи интеграла, распространенного на тело любой формы, может быть легко приведен к только что рассмотренному. Именно, если функция определена в области ,то вместо нее следует лишь ввести, функцию , определенную в объемлющем прямоугольном параллелепипеде , полагая

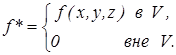
Этим путем и получаются все приводимые ниже формулы.

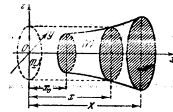
Рис. 2.

Остановимся на случаях, представляющих наибольший интерес. Пусть тело содержится между плоскостями и и каждою параллельною им плоскостью, отвечающей фиксированному значению , пересекается по некоторой фигуре, имеющей площадь; через обозначим ее проекцию на плоскость (рис. 2). Тогда

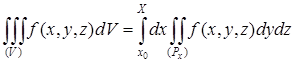(8*)

в предположении существования тройного и двойного интегралов. Это — аналог формулы.

Пусть, далее, тело представляет собой «цилиндрический брус», ограниченный снизу и сверху, соответственно, поверхностями

проектирующимися на плоскость в некоторую фигуру , ограниченную кривой с площадью 0; с боков тело ограничено цилиндрической поверхностью с образующими, параллельными оси , и с кривой в роли направляющей. Тогда аналогично формуле имеем

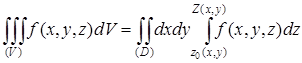
при этом предполагается существование тройного интеграла и простого — внутреннего— интеграла справа.

Если область представляет собой криволинейную трапецию, ограниченную двумя кривыми (рис.14) и и прямыми , , то тело подходит под оба типа, рассмотренных выше. Заменяя двойной интеграл—то ли в формуле, то ли в формуле —повторным, получим

.

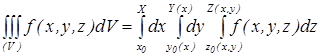Эта формула обобщает формулу.

Как и в простейшем случае, который был рассмотрен в предыдущем п°, и здесь непрерывность функции обеспечивает приложимость всех формул и им подобных, получающихся из них перестановкой переменных .

Рис. 3.

Развитие воспитательной системы
Воспитательная система - не застивший, а постоянно развивающийся феномен. Появляются и исчезают различные идеи, представления, устойчивые способы взаимодействия детей, те или иные виды деятельности, организационные структуры; усложняется и упорядочивается жизнедеятельность коллектива или, наоборот, ...

Пути развития фонематического слуха у детей старшего дошкольного возраста
Основной целью логопедического воздействия при дислалии является формирование умений и навыков правильного воспроизведения звуков речи. Чтобы правильно воспроизводить звуки речи (фонемы), ребенок должен уметь: - узнавать звуки речи и не смешивать их в восприятии (т.е. узнавать звук по акустическим ...

Характеристика мыслительных операций и развитие их в онтогенезе
Мышление - это процесс познания человеком действительности с помощью мыслительных процессов: анализа, синтеза, сравнений и т. п. Анализ-это мыслительное расчленение предмета или явления на образующие его части, выделение в нем, отдельных частей, признаков и свойств. Сравнение - это сопоставление пр ...